Все мы знаем, какой пиздец сейчас происходит с Украиной и одной известной вам страной-победительницей-фашизма. Если вы хотите почитать об этом, помочь актуализировать информацию или высказать свое мнение — можете сделать это в статье Война в Украине и в обсуждении.
Криптография
Эту статью следует переписать
Статью, которая находится перед вами, очень хочется сжечь.
Но мы этого не делаем в надежде, что кто-нибудь сможет ее переписать, спася таким образом от уготованной ей участи.
Указана следующая причина: разделить и дополнить.
На странице обсуждения могут быть подробности.
Тот, кто понял что здесь написано, понял суть криптографии.
Содержание
[убрать]Основные понятия
Для удобства участникам передачи зашифрованного сообщения дают следующие имена: Алиса — отправитель, Боб — получатель, Ева — пассивный перехватчик, Меллори (Man-in-the-middle) — активный перехватчик, может не только перехватывать передачу, но и подменять содержимое.
- Открытый текст — информация, которую отправитель хотел бы передать получателю.
- Криптотекст (также шифротекст, шифрат) — закрытая форма информации. При помощи ключа из криптотекста можно восстановить открытый текст.
- Криптографический алгоритм — ряд математических преобразований, совершаемых над открытым текстом для превращения его в закрытый и наоборот.
- Шифрование (шифр) — способ сокрытия информации, в котором основным элементом является буква. Буквы открытого текста заменяются на другие буквы, числа или символы, либо вместо них подставляются другие буквы, буквенные пары, а иногда более крупные группы букв.
- Криптоанализ (также дешифровка) — изучение криптографического алгоритма с целью получения открытого текста из шифрата без знания ключа. Может производиться ради получения доступа к перехваченным сообщениям. Частным случаем является терморектальный криптоанализ (англ. rubber-hose cryptanalysis, викпдск. бандитский криптоанализ).
- Криптология — наука о методах шифрования и дешифровки.
- Криптоаналитик — агент, которому сообщение не предназначалось, но который стремится дешифровать его.
- Расшифровка — действие, обратное шифрованию: получение открытого текста из шифрата, используя ключ. Не стоит путать с дешифровкой.
- Ключ — это секретная информация, параметр криптографического алгоритма, который используется при шифровании и расшифровке. Все современные криптосистемы построены по принципу Керкгоффса, согласно которому секретность зашифрованных данных определяется секретностью ключа шифрования, то есть даже при известном криптографическом алгоритме криптоаналитик не в состоянии за приемлемое время получить открытый текст, если не располагает ключом.
- Электронная цифровая подпись (ЭЦП) — информация, подтверждающая подлинность другой информации. ЭЦП подобна подписи на бумажном документе: по ней видно, что с документом согласны и видно, кто согласен.
- Криптография с открытым ключом — система из двух ключей: открытого и закрытого. Открытый ключ помещается в публичный доступ, поэтому знание открытого ключа не дает дополнительных возможностей. Асимметричное шифрование: шифруют открытым, расшифровывают закрытым. ЭЦП: шифруют закрытым, расшифровывают открытым.
Асимметричное шифрование используется для передачи данных через прослушиваемый канал, когда требуется уверенность, что только адресат (он же обладатель закрытого ключа) сможет прочитать открытый текст. ЭЦП используется, чтобы подтвердить авторство открытого текста: в этом случае автор шифрует открытый текст своим закрытым ключом, после чего каждый может расшифровать общеизвестным открытым ключом этого автора и проверить открытый текст. Получить шифрат, который бы правильно расшифровывался данным открытым ключом, может только обладатель закрытого ключа. ЭЦП может иметь юридическую силу, подобно обычной подписи, если публичный ключ добавлен в базу данных соответствующего органа.
- Поручитель — человек, подтверждающий принадлежность данного публичного ключа кому-либо. Поручитель является аналогом нотариуса. Поручителю должно оказываться доверие, а его публичный ключ должен быть известен изначально, чтобы с помощью ЭЦП можно было убедиться, что подтверждение выписано поручителем, а не кем-то ещё. Формируются цепочки поручителей разных уровней, в которых публичный ключ следующего подписан предыдущим. У основания стоят поручители с мировым именем, например Verisign. Поручители являются одним из способом гарантировать принадлежность открытого ключа этому человеку, а без этого невозможно направить сообщение, которое мог бы прочитать только адресат, или быть уверенным, что сообщение написано отправителем.
- Хеш-функция — алгоритм, превращающий данные (например, текст) в число (хеш-значение). Число может быть довольно большим, например для md5 это 128-битное число. Криптографическая хеш-функция — это хеш-функция, для которой не существует эффективного способа подобрать такие исходные данные, для которых она выдавала бы заранее выбранный результат. Для некоторых хеш-функций (например, crc32) это требование удается обойти, тогда функция считается взломанной и больше не используется в криптографии. Если появляется алгоритм генерации нескольких текстов, дающих одинаковое хеш-значение, то функцию тоже считают взломанной (например, md5). Криптографическую хеш-функцию можно рассматривать как необратимое шифрование без ключа. Хеш-функции применяются в криптографии для уменьшения размера текста перед его подписыванием ЭЦП и для безопасного хранения паролей, при котором можно проверить соответствие введенного пароля сохраненному, но нельзя узнать сам сохраненный пароль.
Ключ, как правило, можно «приладить» к хеш-функция в виде соли — строки, соединяемой с открытым текстом перед применением хеш-функции. Это бывает полезно для затруднения подбора исходного текста с помощью словарей популярных паролей и таблиц вида текст — хеш-значение. При атаках в качестве такой таблицы может использоваться google. В этом можно убедиться, поискав 202cb962ac59075b964b07152d234b70 — значение хеш-функции md5 для «123». А если использовать соль «wabranes», то md5(wabranes|123) = «477de9d90eaed5064a303698244dc685» уже не находится в гугле (за исключением, возможно, этой страницы).
- Криптографическая стойкость — устойчивость алгоритма и ключей к анализу или перебору, отсутствие в алгоритме уязвимостей. Чем выше стойкость, тем труднее, не имея ключа, совершить действие, для которого он нужен.
История
На протяжении многих столетий коды, шифры, тайные знаки и тайные языки использовались для маскировки информации — сокрытия от посторонних смысла передаваемых сообщений. Со временем потребность в маскировке информации увеличивалась, как и потребность раскрывать чужие секреты. На арене ожесточённого соперничества между теми, кто составляет тайные сообщения, и их противниками, тем, кто пытается разгадать их смысл, родилась криптология.
Древние шифры
Наиболее простейшим является моноалфавитный шифр, известный с глубокой древности. Суть его в том, что буквы одного алфавита, заменяются буквами другого, либо выдуманными символами. Что такой шифр представляет из себя и насколько легко ломается путём обычной логики без применения каких-либо спецсредств, можно прочесть в рассказе «Пляшущие человечки» Конан Дойля.
Одним из классических стал шифр Цезаря, суть которого заключается в том, что каждая буква текста заменяется на букву, номер которой в алфавите отличается от номера исходной буквы на выбранное смещение, например см. начало этой статьи. Это тоже разновидность моноалфавитного шифра, основанного на методе простой замены, то есть замены одной буквы какой-то другой по определённому алгоритму. Стойкость его нулевая, достаточно перебрать все варианты смещения, а их количество равно количеству букв в алфавите и шифр будет легко сломан.
Более продвинутым является греческий шифр «Скитала», он же шифр древней Спарты. На цилиндр наматывалась лента папируса, на которой записывался текст — вдоль цилиндра построчно. Оставшееся незанятым место заполнялось всяким хламом. Если текст не вмещался на одну ленту, использовалась следующая. Если теперь снять ленту с цилиндра, на ней получится внешне бессмысленный набор символов.
Пример:
_________________________________________| | | | | | || | Э | Т | О | Ш | И ||__| Ф | Р | Д | Р | Е |__| В | Н | Е | Й | С | || П | А | Р | Т | Ы | || | | | | | |_________________________________________
Результат: «ЭФВПТРНАОДЕРШРЙТИЕСЫ». Для расшифровки нужно знать диаметр цилиндра. Это пример перестановочного шифра в котором буквы текста меняются местами по заданному алгоритму.
Скремблирование

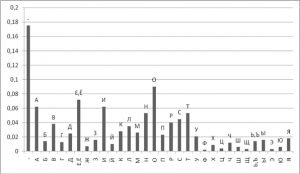
Простые алгоритмы шифрования, например код Цезаря, легко атакуются, если сообщение достаточно длинное и известны частоты букв алфавита. Для этого используется таблицы частот букв, которые составили для всех языков.
На заре криптографии отдельный этап при шифровании уделялся избавлению от неслучайности входного текста. На этом этапе текст накладывался на другой случайный текст (номера букв суммируются, при переходе через последнюю букву алфавита возврат к первой букве алфавита), после чего случайный текст приписывался в начало. Этот этап называется скремблированием. Оно является обратимым шифрованием без ключа, поэтому само по себе открытый текст не защищает, однако приближает его к случайной последовательности, подготавливает для дальнейшего шифрования, затрудняя статистические атаки.
При скремблировании длина сообщения увеличивается незначительно — на длину накладываемого случайного текста. Если же случайный текст не приписывать в начало сообщения и если его длина равна длине сообщения, то такое сообщение абсолютно невозможно восстановить без знания этого случайного текста (при условии, что он был действительно случайным). Ключом служит этот случайный текст. Такой способ шифрования использовался разведчиками для передачи информации государственной важности. Разумеется, ключ можно было использовать только один раз.
Вместо скремблирования по описанному алгоритму можно применить алгоритм сжатия или любой алгоритм, повышающий энтропию текста (похожесть его на случайный).
Когда изобрели блочные шифры (см. ниже), отпала потребность в скремблере. Блочный шифр «засасывает» за раз (то есть, за один блок) достаточно много букв и расхуячивает их внутри блока до полной неузнаваемости. Остается лишь искать статистические зависимости между блоками, что также заходит в тупик, так как один и тот же вход блока дает разный выход в зависимости от номера блока или от содержимого предыдущего блока.
Симметричное шифрование
При симметричном шифровании используется один и тот же ключ для шифровки и для расшифровки. Это влечет за собой ряд проблем. Во-первых, необходим надежный канал для передачи ключа. Во-вторых, группе из N независимых членов потребуется N²/2 симметричных ключей (каждый с каждым), в то время как асимметричных потребовалось бы только N (на каждого по одной паре ключей). В-третьих, симметричное шифрование невозможно использовать для подтверждения авторства (ЭЦП), так как ключ известен обеим сторонам. Зато симметричное шифрование зародилось раньше асимметричного, поэтому лучше изучено. То есть, меньше шансы, что какой-нибудь сумасшедший ученый изобретет эффективную атаку на симметричный алгоритм, чем на асимметричный. Кроме того, симметричные алгоритмы работают быстрее, чем асимметричные, требуют ключ меньшей длины и проще реализуются, в том числе на уровне железа (как AES, к примеру).
Асимметричное шифрование
Метод шифрования, использующий пару ключей, открытый (публичный) и закрытый (секретный), для обмена шифрованными сообщениями. Программа генерирует пару ключей, связанных между собой. Публичный используется только для шифрования, закрытый же — лишь для расшифровки. Ключи связаны между собой так, что невозможно создать ещё один открытый ключ, не имея закрытого. Но воссоздать закрытый ключ, имея публичный, не выйдет даже при наличии образцов исходного и шифрованного текстов. Открытый ключ вместе с данными о его владельце распространяется среди корреспондентов, закрытый же хранится в тайне. Отправитель шифрует сообщение публичным ключом, но расшифровать его может только получатель.
Метод имеет ряд преимуществ перед симметричным шифрованием. При использовании одного ключа для щифрования и расшифровки нужно быть уверенным, что он не попадёт в чужие руки. Следовательно, возникает множество проблем с его хранением и передачей. Пользователь может быть уверен в себе, но не в своих корреспондентах, или каналах связи, через которые он передаёт ключ. Асимметричное шифрование решает проблему сохранности закрытого ключа однозначно, так как при его использовании нет необходимости передавать закрытый ключ всем собеседникам. А публичный может передаваться и даже попасть в руки злоумышленника, но при попытке расшифровки того ждёт фиаско.
Обмен публичными ключами. Уязвимость. Сертификация и сеть доверия.
Если люди уже знаю публичные ключи друг друга — то проблема зашифрованного обмена и подтверждения авторства для них решена (средствами асимметричного шифрования и ЭЦП соответственно). Если обмена ключами не было, но есть гарантия, что сообщения доходят в неизмененном виде (то есть решена задача подтверждения авторства), то средства криптографии с открытым ключом позволяют установить шифрованный канал. А вот наоборот не получится — если мы с кем-то установили шифрованный канал, одного этого недостаточно для уверенности в личности этого человека. Во времена второй мировой главной проблемой криптографии была передача симметричного ключа (который мог разгласить каждый, кто его знал), то сейчас основную сложность представляет обмен публичными ключами. Разглашать публичные ключи бессмысленно, так как они и так находятся в общем доступе, поэтому часть проблем уходит, но открывается достаточно возможностей для подмены самого публичного ключа, что приводит к перехвату шифрованных посланий (подписанных публичным ключом атакующего) или подделке авторства (за автора подписывается атакующий своим публичным ключом). Одним из решений проблемы дополнение схемы поручителями.
Допустим, существует третья заинтересованная сторона, которая предоставит вам свой ключ вместо ключа вашего корреспондента, а ему в свою очередь такой же фиктивный свой ключ вместо вашего. Тогда эта третья сторона сможет расшифровать ваше сообщение, подменить его тем же самым исходным текстом, только зашифрованным настоящим публичным ключом вашего корреспондента, и переслать ему. Он же, обладая вашим фиктивным ключом (который ему заботливо подсунули), шифрует для вас ответ, также достающийся третьей стороне, которая преспокойно добывает исходный текст и шифрует его вашим настоящим ключом. В результате хитрых манипуляций окажется, что вся сложность перехвата сводится не к криптоанализу и созданию идентичных хэшей электронной подписи, что почти невозможно,[2] а к банальной подмене, что вполне реализуемо — было бы сильное желание. Такая атака называется Man-in-the-middle.
Поэтому публичный ключ также имеет защиту от подмены. При его создании необходимо указать имя и адрес электронной почты (можно ник, если переписка анонимная), с помощью которых ваш корреспондент сможет проверить принадлежность имеющегося у него вашего ключа вам. Также у ключа имеется id (номер) и фингерпринт (отпечаток, также хэш, но уже самого ключа, представляющий собой короткую комбинацию, которую нетрудно проверить). Злоумышленник может сгенерировать свою пару ключей и вписать в публичный ваше имя и адрес электронной почты, но его фингерпринт будет отличаться от вашего. Получив чей-либо ключ из ненадёжного источника, можно легко проверить его, попросив корреспондента прислать его фингерпринт, используя альтернативный способ связи (по телефону или через im). После чего достоверность владения соответствующим закрытым ключом будет равна достоверности выбранного альтернативного способа связи.
Существуют сети доверия, когда, проверив публичный ключ, поручитель подписывает его, и все, кто доверяет этому поручителю, будут считать, что оный принадлежит именно тому, с кем они хотят иметь дело, а не третьей стороне. При этом они сами могут проверить этот ключ вышеуказанным способом. Существуют и государственные сертификационные центры, где можно регистрировать ключи. За некоторую сумму они согласятся выдавать ваш публичный ключ и персональные данные любой требующей подтверждения стороне. Система сертификационных центров, широко эксплуатируемая на государственном уровне и в интернет-торгах, использует набор программного обеспечения X.509, работающий на основе тех же алгоритмов. Но их ПО является коммерческим и закрытым?, а основная задача — создание и заверение электронных подписей, а не криптография.
Алгоритмы симметричного и асимметричного шифрования, а также ЭЦП реализованы в программном обеспечении PGP.
Квантовая криптография
Это новое направление в криптографии, основанное не на математических методах, как обычная, а на принципах квантовой механики.
Осторожно, квантовая механика!
Этот раздел содержит зашкаливающее количество квантовой механики. Если вы не доктор наук, вы вряд ли поймёте то, что здесь написано. Если вы доктор наук, можете помочь проекту, добавив сюда ещё больше квантовой механики
Основы квантовых вычислений
В обычном компьютере информация хранится в виде битов, такое двоичное представление упрощает большинство внутренних преобразований, которые компьютер должен выполнить перед началом вычислений. Так, например, число 15 будет храниться в виде 1111, а число 10 как 1010. Так как любое число X может быть представлено с помощью приблизительно log2X
Квантовый бит, или кубит, основан на фундаментальном понятии о суперпозиции квантовых состояний. Рассмотрим парадокс кошки Шрёдингера. Поместим кошку в ящик со стабильным радиоактивным источником. Кошка погибнет, если подвергнется воздействию излучения. Фактически кошка либо мертва, либо жива, независимо от того, посмотрим ли мы в ящик или нет, но согласно квантовой механике она одновременно и жива, и мертва, кошка существует в суперпозиции из мертвого и живого состояний. До тех пор пока мы не заглянем внутрь ящика, мы должны рассматривать кошку как существующую в трансцендентной неопределённости. Мы можем лишь утверждать, что есть определённая вероятность, что кошка жива, и определённая вероятность, что она мертва. Это называется амплитудой вероятности.
Этот парадокс можно использовать для того, чтобы дать понятие о кубите. Кубит — это кошка. Если кошка мертва, то это состояние обозначается как 0, а если жива, то 1. Так как кошка ни жива, ни мертва, то она находится одновременно в двух этих состояниях. В этом смысле два числа (0 и 1) означают использование только одного кубита. В классическом виде это изображается двумя битами, один символизирует смерть (0), а второй — жизнь (1).
Квантовый компьютер манипулирует кубитами таким образом, что вероятность измерения верного исхода возрастает в процессе вычислений. Информация должна храниться в квантовом состоянии, которое изолировано от окружающей среды. Наилучший вариант на сегодня это использование ядерного спина — квантового аналога момента вращения волчка, способного хранить информацию около секунды.
Квантовая когерентность — это мера взаимодействия между компьютером и окружающей средой. Ядерный спин может находиться в одном из многих квантовых состояний, информация о которых просачивается наружу, если они взаимодействуют с окружающей средой. Квантовые состояния теряют частоту, и как следствие, теряют способность интерферировать. Интерференционные картины содержат относительную информацию о конфигурации квантовых битов, и именно поэтому они являются основой большинства теорий квантовых вычислений.
Криптография
Одно из направлений квантовой криптографии заключается в передаче информации с использованием состояний, которые защищены от перехвата и подслушивания благодаря физическим законам. Описание различных методов квантовой криптографии есть в статье Доминика Майерс и Эндрю Яо «Безусловная стойкость в квантовой криптографии» [3]
В этой статье основной протокол основывается на предположениях, выдвинутых в 1970 году С. Виснером и Ч. Беннетом и Ж. Брассардом в 1984 году. Для того чтобы понять как это работает, рассмотрим следующий пример:
Пусть Алиса — отправитель, а Боб — адресат. Алиса может посылать фотоны с одной из четырёх возможных поляризаций: 0, 45, 90 или 135°. Поляризация означает, что электромагнитное поле фотона ориентировано в определённом направлении, согласно квантовой механике, детектор может распознавать фотоны с поляризацией 0 и 90° или 45 и 135°. Так как эти состояния неизменны, невозможно распознать оба типа одновременно.
Чтобы договориться о ключе, Алиса передаёт серию фотонов со случайно выбранной поляризацией. Для каждого из фотонов Боб произвольно выбирает вид измерения (0-90° или 45°-135°), а затем записывает результат, сообщает Алисе о том порядке, в котором он производил измерения, а та говорит ему, какие измерения были верными. Для всех измерений Алиса и Боб выписывают ряд единиц и нулей в зависимости от того, был ли посланный сигнал 0 и 90° или 45 и 135°. Этот ряд цифр в дальнейшем и используется как ключ. Так как, согласно квантовой механике, невозможно наблюдать какое-либо состояние, не изменив его и не поменяв поляризацию, любой, кто захочет перехватить сообщение, изменит и переданные фотоны, после чего у Алисы с Бобом уже не будет одинакового ключа. Открыто обсудив случайно выбранное подмножество цифр ключа, Алиса и Боб могут проверить, не перехватывают ли их сообщения. Убедившись, что всё в порядке, они могут продолжить передавать информацию, зашифрованную этим ключом.
Криптоанализ
В процессе поиска новых криптометодов в области квантовой криптографии открылись новые возможности. Так, например, с её помощью можно за обозримое время найти простые делители большого числа, что делает несостоятельной криптосистему RSA. К счастью, неизвестен подобный алгоритм классической информатики. На текущий момент одним из самых быстрых классических компьютерных алгоритмов разложения числа на множители является решето числового поля. Им можно произвести разложение числа из X цифр на множители за время, экспоненциально растущее как X в степени 1/3, в то время как последние квантовые алгоритмы теоретически позволяют разлагать числа на множители за время, пропорциональное X², проще говоря, квантовый компьютер, выполняющий всего 100 вычислений в секунду (что очень мало) разложил бы на множители число из 100 цифр примерно за 2-3 минуты, в то время как сегодня самое большое число, когда-либо разложенное на множители, имеет 155 знаков, а само разложение потребовало совместной работы 292 компьютеров в течение семи месяцев.